Découvrir le courant électrique
Pourquoi des matériaux (notamment les métaux) conduisent-ils de l'électricité ?
Nous avons vu que l'atome selon le modèle de Bohr, proposait des électrons sur des orbites situées à une certaine distance du noyau . Pour être conducteur, l'atome doit libérer facilement des électrons libres. Les seuls candidats possibles sont les candidats de la dernière couche de l'atome. Prenons le cas d'un atome de cuivre, un très bon conducteur. Vous observerez qu'il ne dispose que d'un seul électron sur sa dernière couche. Ce dernier électron deviendra, suite à l'agitation thermique de l'atome, un électron libre. C'est cet électron libre qui pourra se déplacer et engendrer un courant électrique dans le matériau. \(\newline\)

La figure ci-dessous montre l'énergie à apporter pour passer de la bande de valence (électrons associés à d'autres atomes par liaison covalente) à la bande de conduction. Vous observerez que pour les métaux ces deux bandes se chevauchent. Ce qui signifient que des électrons libres sont disponibles dans le matériau à 25 °C. \(\newline\)
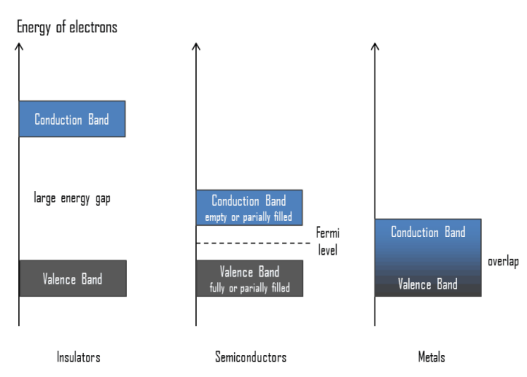
Remarque :
Pour les semi-conducteurs, le niveau de Fermi est une fonction de la température mais il peut être considéré, en première approximation, comme une constante, laquelle équivaudrait alors au niveau de plus haute énergie occupé par les électrons du système à la température de 0 K. Ce semi-conducteur pourra donc dans certaines circonstances devenir conducteur. \(\newline\)
Pour les isolants, il faudra fournir une tension énorme pour les rendre conducteurs. Généralement cela provoque un arc et condamne le matériau. c'est également ce qui se passe lors d'un orage lorsque l'air devient conducteur. On dit alors que l'isolant claque. \(\newline\)
Définition : Le courant électrique
Le courant électrique sera défini comme le débit de charges circulant à l'intérieur du conducteur. On notera : \(\newline\)
\(I (Ampères)= {{\Delta Q (coulombs)} \over {\Delta t (secondes)}}\) \(\newline\)
Si on fait la limite de cette quantité on obtient :
\(I = \lim\limits_{\Delta t \to 0}\) \({{\Delta Q} \over {\Delta t}} = {{dQ} \over {dt}}\) \(\newline\)
Le saviez vous ?
La charge d'un électron vaut 1,6×10−19 Coulombs. \(\newline\)
Complément :
Pour calculer le nombre d’électrons libres disponibles dans un fil de cuivre, on suit les étapes suivantes :
1. Données connues :
Section du fil : S=2,5 mm2
Longueur : L=10 cm=0,1 m
Volume du fil : V=S×L=2,5×10−6×0,1=2,5×10−7 m3
Densité du cuivre : ρ=8,96×103 kg/m3
Masse molaire du cuivre : M=63,5 g/mol=0,0635 kg/mol
Constante d’Avogadro : NA=6,022×1023 atomes/mol
Nombre d’électrons libres par atome de cuivre : 1 (le cuivre a 1 électron de conduction)
2. Calcul de la masse du fil :
m=ρ×V=8,96×103×2,5×10−7=2,24×10−3 kg
3. Nombre de moles de cuivre :
n=m×M=2,24×10−3 . x 0,0635 ≈ 3,53×10−2 moles
4. Nombre d’atomes de cuivre :
Natomes=n×NA=3,53×10−2×6,022×1023≈2,13×1022 atomes
5. Nombre d’électrons libres :
Puisque chaque atome de cuivre fournit 1 électron libre :
Nélectrons libres=Natomes≈2,13×1022 électrons
\(\newline\)
Fondamental :
On remarque, que dans un conducteur il y a un nombre impressionnant d'électrons libres. C'est comme avoir un récipient fermé avec plein d'eau à l'intérieur. Comme une seringue remplie. Comment faire sortir ces électrons du conducteur ? Il faut exercer une « pression » électrique et cette « pression » se nommera la tension électrique. » \(\newline\)