Comprendre ce qu'est une résistance électrique
Prenons un conducteur, alimenté par une pile. Cette pile impose une différence de potentiel électrique entre les deux extrémités.\( \newline\)
Le conducteur est de section S et de longueur L. Les électrons libres sont accélérés par le champ électrique E.\( \newline\)
En effet la force électrostatique vaut \(F = e \cdot E\). D'après la seconde loi de Newton \(F = m \cdot a\).\( \newline\)
Dans le vide un électron libre serait accéléré à \(a= e/m \cdot E\). La vitesse pourrait devenir infinie. C'est ce principe qui est utilisé dans les accélérateurs de particules sur les portions droites.\( \newline\)
Dans la réalité nos électrons libres vont heurter les atomes et donc être fréquemment ralentis puis être accélérés par le champ électrique E. \(\newline\)
Si l'on considère la force de frottement on peut écrire que \(F_f = -k'\cdot v\).\( \newline\)
La seconde loi de Newton permet d'écrire \(F_e-F_f = m\cdot a\). L'accélération s'annule quand \(F_e=F_f ~soit~ e\cdot E = k' \cdot v\).\( \newline\)
La vitesse limite sera donc \(v = e/k'\cdot E\). Ainsi la vitesse de dérive globale des électrons vaudra \(v_d = \mu\cdot E\).\( \newline\)
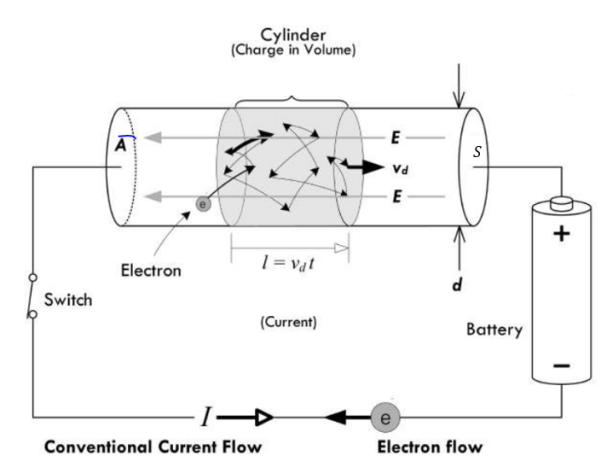
Considérons la charge contenue dans le volume \(\Delta V = S\cdot l = S\cdot v_d\cdot t\).\( \newline\)
La charge contenue dans ce volume vaut \(~\Delta Q = n \cdot e \cdot \Delta V\) soit \(~\Delta Q = n \cdot e \cdot S\cdot v_d\cdot \Delta t\) ou \(~\Delta Q = n \cdot e \cdot S\cdot \mu \cdot E \cdot \Delta t\).\( \newline\)
Par définition \(I = {{\Delta Q} \over {\Delta t}}\),\( ~I = \mu \cdot n\cdot e\cdot S \cdot {{U} \over {L}}\).\( \newline\)
Posons \(\rho = { {1} \over {\mu \cdot n\cdot e} }\).\( \newline\)
Cela donne \(I = { {S} \over {\rho \cdot L} } \cdot U\) ou \(U = { {\rho \cdot L} \over {S} } \cdot I \).\( \newline\)
Donc avec\( ~R= { {\rho \cdot L} \over {S} }\) .\( \newline\)
\(U = R \cdot I \), c'est la loi d'ohm.\( \newline\)
Fondamental :
Ainsi la résistance électrique est liée à la vitesse de dérive des électrons dans le conducteur. Si cette vitesse est faible,\( ~\mu~ \)est faible et la résistance est élevée. \(\newline\)
Plus le fil est long, plus les collisions se multiplient, ce qui ralentit les électrons et augmente la résistance. \(\newline\)
Augmenter la section du fil permet de mieux écouler le courant électrique, ce qui diminue la résistance électrique. \(\newline\)
Remarque :
Levons une idée qui est souvent confuse dans l'esprit de beaucoup. Ce ne sont pas les électrons eux-mêmes qui transportent l'énergie électrique ! Calculons la vitesse de dérive pour un courant de un ampère dans un conducteur de 2.5 mm2. \(\newline\)
Calculons la vitesse de dérive vd des électrons dans un fil de cuivre de section 2,5 mm² parcouru par un courant de 1 A. \(\newline\)
Formule de la vitesse de dérive :\( \newline\)
\(v_d = \frac{I}{n \cdot e \cdot S}\)\( \newline\)
où :\( \newline\)
I=1A : courant.\( \newline\)
n=8,5×1028 électrons/m3 : densité d’électrons libres (nombre d’électrons libres par m³), ce qui est très élevé !.\( \newline\)
e=1,602×10−19 C : charge élémentaire.\( \newline\)
S=2,5×10−6 m2 : section du conducteur.\( \newline\)
Calcul de la vitesse de dérive vd ≈ 2,94×10−5 m/s. Cette vitesse est très faible ! La vitesse de dérive des électrons dans un conducteur est généralement très lente, de l'ordre de quelques millimètres par seconde, voire quelques centimètres par heure dans un fil de cuivre. Cependant, le champ électrique se propage très rapidement, presque à la vitesse de la lumière, ce qui explique pourquoi les circuits réagissent presque instantanément aux changements. Cette distinction est importante car la vitesse de dérive fait référence au mouvement des électrons eux-mêmes, tandis que la vitesse de propagation du champ électrique est liée à la transmission des signaux électromagnétiques. En d'autres termes, les électrons se déplacent lentement, mais le signal électrique, qui est transmis par le champ électrique, se propage très rapidement. Cette différence peut être illustrée par l'analogie d'un tuyau d'arrosage déjà plein d'eau : lorsque le robinet est ouvert, l'eau sort immédiatement de l'autre extrémité, même si les molécules d'eau ne se déplacent que lentement.\( \newline\)
Fondamental :
Alors d’où vient l’énergie ?\( \newline\)
L’énergie circule dans le champ électromagnétique créé par la combinaison du :\( \newline\)
Champ électrique (produit par la pile ou le générateur),\( \newline\)
Champ magnétique (produit par le courant lui-même).\( \newline\)
L’énergie n’est pas contenue dans les électrons, mais dans les champs qui se forment autour du fil, et qui propulsent l’énergie jusqu’aux appareils (lampe, moteur…).\( \newline\)
Un exemple d'ingénierie défaillante
Le câble transatlantique de 1858 : un échec instructif.\( \newline\)
Contexte :\( \newline\)
Premier câble sous-marin transatlantique installé entre l’Irlande et Terre-Neuve (env. 4000 km).\( \newline\)
Objectif : transmettre des messages télégraphiques entre l’Europe et l’Amérique.\( \newline\)
Inauguré en août 1858, il fonctionna quelques semaines seulement.\( \newline\)
Problèmes rencontrés :.\( \newline\)
Signal très faible à l’arrivée :\( \newline\)
Le courant envoyé à une extrémité mettait des secondes à produire un effet à l’autre bout.\( \newline\)
Cela était dû à une forte capacitance du câble (le cuivre était entouré de gutta-percha, un isolant naturel).\( \newline\)
Ce système se comportait comme une ligne de transmission avec effet capacitif et inductif, mais les ingénieurs de l’époque n’avaient pas encore ce modèle en tête.\( \newline\)
Tentative de "forcer le signal" :\( \newline\)
Pour compenser la faiblesse, les opérateurs ont augmenté la tension, espérant un meilleur signal.\( \newline\)
Cela a endommagé l’isolation du câble — le câble a grillé intérieurement.\( \newline\)
Mauvaise compréhension du rôle du champ électromagnétique :\( \newline\)
À l’époque, les ingénieurs pensaient encore le courant comme un flux de fluide.\( \newline\)
Ils n’avaient pas encore pleinement intégré les notions de vitesse de propagation du signal, réflexion, impédance, etc..\( \newline\)
James Clerk Maxwell n’avait pas encore publié ses équations définitives.\( \newline\)
Ce qu’on comprend aujourd’hui (et que l’on ignorait alors) :\( \newline\)
Dans un câble long, le courant ne s’installe pas instantanément.\( \newline\)
Le signal électrique se propage à travers les champs électromagnétiques autour du câble, pas "dans" le cuivre.\( \newline\)
Le câble agit comme une ligne de transmission :\( \newline\)
Il a une capacité (entre le conducteur et l’eau autour),\( \newline\)
Une inductance (à cause du champ magnétique produit par le courant),\( \newline\)
Et une résistance du conducteur.\( \newline\)
Pour éviter les réflexions et pertes, on doit adapter l’impédance et limiter la bande passante.\( \newline\)
Leçon importante :\( \newline\)
Le mauvais fonctionnement du câble ne venait ni du cuivre, ni des électrons, mais d’une mauvaise compréhension du champ électromagnétique et de la physique de la transmission du signal.\( \newline\)