Les lois de Kirchhoff
Les lois de Kirchhoff
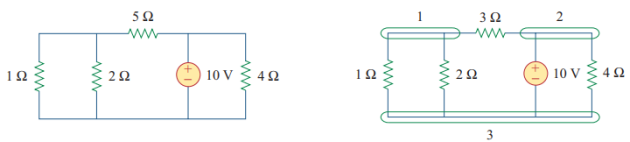
Trouver le nombre de nœuds, c'est identifier dans le circuit les équipotentielles, c'est à dire tous les points qui partagent la même tension. Ce repérage laisse apparaître des branches. Une maille sera définie comme une succession de branches formant un circuit fermé (cf boucle 1 et boucle 2). \(\newline\)
Les lois de Kirchhoff stipulent que :
La somme des courants entrant par un nœud est égale à la somme des courants sortant par le même nœud. (Conservation de la charge électrique).
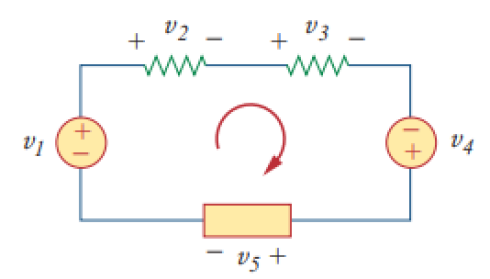
La loi des tensions de Kirchhoff stipule que la somme algébrique des tensions le long d’une maille est constamment nulle. Les tensions rencontrées lors du parcours de la maille sont positives si elles s'alignent sur ce parcours et négatives si elles s'y opposent. (Conservation de l'énergie).\(\newline\)
Cette dernière provient du fait que le parcours d'un champ électrique sur un circuit fermé signifie que la tension est nulle. En effet \(U = E \cdot L = V_a - V_b\). Si la longueur du parcours est nulle (circuit fermé : le point A correspond au point B) la différence de potentiel (et donc la tension) est nul.\( \newline\)
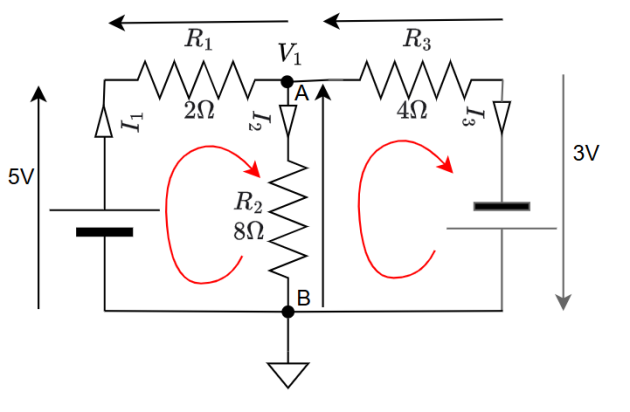
Reprenons notre exemple avec le courant\(~ I_1\) correctement positionné. \(\newline\)
L'application des lois de Kirchhoff donne :
nœud A : \(I_1 - I_2 - I_3 = 0\)
boucle 1 : \(5 - V_{2\Omega} - V_1= 0\)
boucle2 : \(V_1 - V_{4\Omega} +3= 0\)
L'application de la loi d'ohm donne :
\(2\Omega : V_{2\Omega} = 2 \cdot I_1\)
\(8\Omega : V_1 = 8 \cdot I_2\)
\(4\Omega : V_{4\Omega} = 4 \cdot I_3\)
Le système devient :
nœud A : \(I_1 - I_2 - I_3 = 0 \text~(1)\)
boucle 1 : \(5 - 2 \cdot I_1- 8 \cdot I_2= 0 \text~(2)\)
boucle2 : \(8 \cdot I_2 - 4 \cdot I_3+3= 0 \text~(3)\)
\(\newline\)
Méthode de résolution par substitution
\(\newline\)Étape 1 : Isoler \(I_1\) dans l’équation (1) \(\newline\)
\(I_1 = I_2 + I_3 \quad \text{(Éq. 1')}\)
\(\newline\)Étape 2 : Remplacer \(I_1\) dans l’équation (2) \(\newline\)
\(5 - 2 \cdot (I_2 + I_3) - 8 \cdot I_2 = 0 \\ 5 - 2 \cdot I_2 - 2 \cdot I_3 - 8 \cdot I_2 = 0 \\ 5 - 10 \cdot I_2 - 2 \cdot I_3 = 0 \\ \Rightarrow 10 \cdot I_2 + 2 \cdot I_3 = 5 \quad \text{(Éq. 2')}\)
\(\newline\)Étape 3 : Simplifier l’équation (2') \(\newline\)
\(5 \cdot I_2 + I_3 = 2.5 \quad \text{(Éq. 4)}\)
\(\newline\)Étape 4 : Simplifier l’équation (3)\(\newline\)
\(8 \cdot I_2 - 4 \cdot I_3 + 3 = 0 \\ \Rightarrow 8 \cdot I_2 - 4 \cdot I_3 = -3 \quad \text{(Éq. 5)}\)
\(\newline\)Étape 5 : Résoudre le système formé par les équations (4) et (5) \(\newline\)
Éq. (4) : \(\newline\)
\(5 \cdot I_2 + I_3 = 2.5 \Rightarrow I_3 = 2.5 - 5 \cdot I_2 \quad \text{(Éq. 6)}\)
\(\newline\)Remplacer dans Éq. (5) : \(\newline\)
\(8 \cdot I_2 - 4(2.5 - 5 \cdot I_2) = -3 \\ 8 \cdot I_2 - 10 + 20 \cdot I_2 = -3 \\ 28 \cdot I_2 - 10 = -3 \\ 28 \cdot I_2 = 7 \\ I_2 = \frac{1}{4} \text{ A}\)
\(\newline\)Étape 6 : Trouver I_3 \(\newline\)
Avec Éq. (6) :
\(I_3 = 2.5 - 5 \cdot \frac{1}{4} = 2.5 - 1.25 = 1.25 \text{ A}\)
\(\newline\)Étape 7 : Trouver I_1 \(\newline\)
Avec Éq. (1') :
\(I_1 = I_2 + I_3 = \frac{1}{4} + \frac{5}{4} = \frac{6}{4} = 1.5 \text{ A}\)
\(\newline\)Résultats finaux :
\(\boxed{I_1 = 1.5\ \text{A},\quad I_2 = 0.25\ \text{A},\quad I_3 = 1.25\ \text{A}}\) Comme\( V_1 = 8 \cdot I_2 ~\boxed{V_1 = 2~Volts}\) \(\newline\)
\(\newline\)Méthode de résolution par matrice avec Matlab\(\newline\)
\(\left\{\begin{eqnarray} I_1−I_2−I_3 & = & 0 \\ −2 \cdot I_1−8 \cdot I_2 & = & −5 \\ 8 \cdot I_2−4 \cdot I_3 & = & −3 \end{eqnarray}\right . \newline\)
\(\begin{bmatrix} 1 & -1 & -1 \\ -2 & -8 & 0 \\ 0 & 8 & -4 \end{bmatrix} \cdot \begin{bmatrix} I_1 \\ I_2 \\ I_3 \end{bmatrix} = \begin{bmatrix} 0 \\ -5 \\ -3 \end{bmatrix}\) on a \(B = A \cdot I \). Pour obtenir I il faut calculer I = \(A^{-1} \cdot B\).
\(\newline\)
Dans Matlab saisir :
\(\newline\)
A = [1 -1 -1;-2 -8 0;0 8-4]; \(\newline\)
B = [0 ;-5 ;-3]; \(\newline\)
I = A \ B \(\newline\)
A voir l'outil de résolution de systèmes d'équations avec la calculatrice.\( \newline\)